Une adaptation de saison du célèbre « bon panier » de Joël Briand pour amener les élèves à comprendre le sens de l’addition.
Les situations mathématiques, selon Joël BRIAND
Faire des mathématiques, c’est construire un modèle donc :
– résoudre un problème : anticiper, émettre des hypothèses, faire des essais, les valider ou non, verbaliser
– s’entrainer
– apprendre et retenir
Joël BRIAND précise que souvent, dans les classes, nous avons plus d’activités d’entrainement, de consolidation que de réelles situations problèmes. Souvent l’apprentissage se fait par familiarisation, l’enfant comprenant le problème et cherchant à le résoudre. Briand amène à réfléchir sur les dispositifs permettant de questionner les élèves.
Pour cela, il faut interroger nos situations mathématiques afin de voir si elles comprennent des situations clés permettant un apprentissage par adaptation.
• Y a-t-il bien un problème posé aux élèves ou ont-ils seulement à appliquer une consigne ?
• Résolvent-ils le problème avec une connaissance déjà acquise ou doivent-ils en construire une nouvelle ?
• Peuvent-ils comprendre la consigne et s’engager dans la résolution du problème sans disposer de cette nouvelle connaissance ?
• Le matériel permet-il la validation ? Comment voient-ils qu’ils ont réussi ou échoué ?
• La vérification du résultat permet-elle de lui donner des aides sur la façon de réussir ?
• Peuvent-ils faire plusieurs tentatives ?
• L’échange des points de vue est-il prévu ?
Dans nos séquences d’apprentissage, nous devrions donc retrouver des situations de ce genre mais aussi des activités d’entrainement, de consolidation.
Pour ce genre de situations problèmes, je ne peux que vous orienter vers le groupe ERMEL et leur livre ERMEL GS , le livre de Fabien EMPRIN chez CANOPE ou Maths à Grand PAS.
La situation du PANIER – 1 ère séance
Adaptée à l’époque de Noël …pour amener les élèves à passer du nombre au calcul.
Voici les documents en pdf : bon hotte BRIAND, hotte- BRIAND
Consigne et phase de recherche des élèves
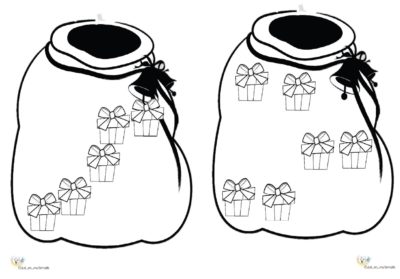
J’ai mis en place cette situation avec un petit groupe de 8 GS. Voici la consigne : « Je donnerai à chaque enfant un message comme celui. Il vous servira à colorier les cadeaux dessinés dans les hottes. Mais attention, il faudra chercher la bonne hotte pour pouvoir colorier tous le cadeaux en suivant le message ».
Chaque enfant reçoit donc un bon de commande. Les hottes sont étalées au fond de la classe, avec des crayons de couleurs à disposition. Les enfants choisissent une hotte et colorient les cadeaux selon le bon de commande.
Quand tous les enfants ont fini, nous regardons ensemble les hottes coloriées.
Lors de la première fois, pour permettre aux élèves de s’approprier la situation, il est possible de donner des hottes correspondant tout à fait à un bon de commande (cf les variables). Mais il faut très vite les enlever, afin de poser aux élèves un problème qui va les amener à construire une nouvelle connaissance (l’addition).
Plusieurs variables :
– la possibilité ou non de prendre son bon de commande avec soi
– la disposition des cadeaux dans les hottes : en lien avec le bon de commande (3 d’un côté, 2 de l’autre ou alors 5 regroupés dans un coin)
– la quantité globale sur le bon de commande
Validation et mise en commun
La validation se fait par l’enfant lui-même et grâce au matériel : mes cadeaux sont-ils tous coloriés ? le bon de commande et s-il respecté ?
La mise en commun permet à chacun de verbaliser sa réussite ou non mais surtout sa stratégie.
« J’ai cherché 3 et 2 dans ma hotte. J’ai vu 3 et 2. Moi j’ai regardé, là si j’ai 4 en jaune, il m’en reste, ça ne va pas, je dois en avoir 2. »
A la fin de cette première mise en commun, la stratégie additive n’a pas été évoquée par les enfants. Ils sont restés sur 2 quantités distinctes. Mais ils verbalisé et ont compris que « 3;2 est pareil que 4;1 ».
Une deuxième séance parait nécessaire pour amener les élèves à atteindre la stratégie experte.
Lors de la première mise en commun, je ne mets en avant aucune procédure, afin de permettre à chacun de s’approprier celle qui lui convient, celle qu’il est capable de mettre en œuvre.
Une surprise lors de cette première séance : un enfant que je pensais très performant en maths (qui dénombre de grandes quantités, qui mémorisent facilement les quantités, qui connait des doubles, décompose des quantités) est resté bloqué avec son bon de commande. Il cherchait 3 et 2 mais n’a pas trouvé de hottes avec cette disposition. Il n’a pas réussi à passer au-dessus de cette première idée et d’ajouter les 2 quantités.
Pour plus de détails sur cette situation, je vous conseille la lecture du GUIDE MATHS sur Eduscol p. 43 ou la conférence de Joël BRIAND sur le centre Alain Savary ou des compte-rendus.
Le bon panier – 2 ème séance
Même consigne, même dispositif. Lors de la mise en commun, un élève explique qu’il a utilisé ses doigts pour trouver « 3 et 2 ben ça fait 5 ! »
Pour mettre en avant cette procédure, nous avons compté les cadeaux dans les hottes et vu que plusieurs hottes étaient identiques mais que les bons de commandes étaient différents. « Oui maitresse, ça, ça fait 5 , et ça aussi ! »
Dans quelques jours, la séance suivante.












Cette année j’essaie justement de proposer plus de situations problèmes à mes GS, je suis consciente que mon enseignement en manquait jusqu’à présent ! J’ajoute cette idée à ma liste à faire la semaine prochaine !!! Merci beaucoup pour toutes ces ressources !
Merci pour cette séance, ça a l’air top! je viens de créer le même type de séance sur le thème des rois et des reines. Trouver la bonne couronne!! j’espère que ça plaira aux élèves.
Merci beaucoup pour votre lecture. On peut en effet changer facilement l’emballage de cette situation en gardant le même objectif. Il faut alors faire attention à la disposition des joyaux sur les couronnes : par paquet comme sur le bon de commande ou totalement autrement.