Les algorithmes

Continuer un collier, compléter une chenille avec des gommettes, activités que nous faisons tous dans nos classes … mais pourquoi ? Quels objectifs ont-elles vraiment dans le développement des enfants ?

Cet article arrive après avoir assisté à une agora d’Yves Thomas, co-auteur de Maths à grands pas, au congrès AGEEM à Bressuire. J’ai complété ses propos en lisant plusieurs articles, documents sur internet et en échangeant avec Fabien Emprin, co-auteur entre autres de Enseigner les mathématiques en maternelle mais aussi mon prof de maths à l’IUFM 😉

A aucun moment, je ne me considère aussi experte que ces personnes sur le sujet, je rassemble juste ici des idées qui me paraissent intéressantes et pertinentes quant aux activités sur les algorithmes, faites en classe.

Un algorithme, mais qu’est-ce que c’est ?

Le mot « algorithme » vient du nom de l’auteur persan Al-Khuwarizmi (né vers 780 – mort vers 850).
Un algorithme est une suite finie de règles à appliquer dans un ordre déterminé à un nombre fini de données pour arriver, en un nombre fini d’étapes, à un certain résultat et cela indépendamment des données.

Les algorithmes en classe

En maternelle, nous travaillons plus les algorithmes sous formes de suite logiques (suites organisées – IO). Dominique Pernoux distingue deux types de suites algorithmiques :

• les plus « simples » sont les suites algorithmiques répétitives comme par exemple :
Δ Ο Δ Ο Δ Ο Δ Ο Δ Ο…

• les plus « complexes » sont les suites algorithmiques récursives comme par exemple :
Ο Δ Ο Ο Δ Ο Ο Ο Δ Ο Ο Ο Ο Δ ……
(la récursivité, qui permet de définir successivement chacun des objets de la suite à partir des objets précédents joue un rôle important en mathématiques et en informatique…)

Les suites « ♣ Δ Δ ♣ Δ Δ ♣ Δ Δ ♣ Δ Δ ….. » et « tambour cloche cloche tambour cloche cloche tambour … » sont isomorphes : elles ont la même structure.
La notion d’isomorphisme est très importante en mathématiques car elle permet d’aller vers plus d’abstraction en dégageant des structures communes à des objets à priori de natures différentes.

Pourquoi travailler les algorithmes ?

Pourquoi nous demande-t-on (et donc demandons-nous aux enfants) de travailler les algorithmes ? Quel intérêt pour eux ? Quelle continuité au cycle 2 ?
Mathématiquement parlant, ils ne les utiliseront qu’en Première option Maths !!! Là où est réellement utilisé le concept de suites mathématiques. Pourquoi les aborder si tôt alors … ? Un résidu des Maths Modernes (enseignées à l’école primaire il y a bien longtemps 😉 ), idée selon laquelle on enseigne les maths à partir de ses structures de base (topologie, algorithme …). Première interrogation !

Deuxième interrogation, mise en avant par Yves Thomas dans son agora :  voici 3 propositions pour continuer un même algorithme  (rouge- vert- rouge – vert) et aucune n’est fausse !

En effet, il y a énormément d’implicite dans la continuité de la suite. Quand nous travaillons ainsi les suites organisées (compléter un collier, poursuivre un collage de gommettes ou de papiers…), nous souhaitons développer chez nos élèves la mémorisation d’une suite d’opérations, la logique d’une suite.
Mais rien n’empêche d’avoir une autre logique :
– alterner les couleurs (réponses attendues par l’enseignant)
– continuer à l’identique de la dernière perle
– changer la couleur à chaque fois

Comment les faire évoluer ?

Yves Thomas propose une manière plus ambitieuse de travailler les suites logiques.

Ainsi en proposant de voir puis de cacher la suite logique, l’enfant doit la mémoriser puis la reproduire.

Il est ensuite possible de complexifier la tâche avec des enchainements plus complexes à mémoriser.

1. suite du style ABC ABC
2. 9 bleues – 6 rouges
3. 3 rouges – 1 bleue / à gauche et à droite puis compléter avec des rouges
4. alterner rouge bleue – augmenter les quantités 1, 2, 3, …
5. beaucoup plus complexe 😉

Si vous souhaitez lire son article en entier, c’est ICI

Une autre manière d’aborder les suites logiques serait de les travailler afin d’amener les élèves à identifier un critère logique. Pour cela il faut proposer une suite avec plusieurs critères (forme – taille – couleur).

Par exemple, une suite comme

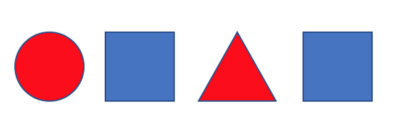permet de faire réfléchir les élèves et de les amener à déterminer un critère : on continue en alternant soit la couleur soit les formes.
Il semble donc intéressant de créer des algorithmes permettant plusieurs suites possibles et ainsi engager un échange entre les élèves.

Cette activité est à travailler chez les MS et les GS, les PS pouvant déjà s’entrainer sur des algorithmes à un seul critère.

Et au-delà des algorithmes …

Travailler les algorithmes de manière plus poussée et donc amener les élèves à trouver le critère de la suite leur permet aussi de dépasser la pensée syncrétique.
Le syncrétisme est la tendance spontanée des enfants à percevoir par visions globales au lieu de discerner les détails (tout est dans tout). Il est leur difficile de catégoriser, de comprendre qu’un objet peut avoir plusieurs critères. Chercher un critère dans une suite logique va les amener à surmonter cet obstacle à l’apprentissage.

Et n’oublions pas, les algorithmes, les suites logiques, les enchainements d’actions sont à relier à la programmation, au codage. Activités que l’on peut faire avec la BeeBot ou Scratch Junior … mais ce sera lors d’un autre article ! 😉

J’espère que cet article est clair et vous aura permis d’éclaircir les objectifs des algorithmes.

Si vous souhaitez aller plus loin, voici quelques écrits que je trouve intéressants :
article de l’ IREM de la Réunion  : de la suite logique au codage
initiation à l’algorithmique et à la programmation C1-C2-C3 (académie de Reims)
Mathématiques en maternelle activités logiques (D. Pernoux)
algorithmique au lycée

 

 

 

 

algorithme didactique maths